Como fazer divisão com virgula?

Como fazer a divisão de um número inteiro por um número com vírgula?

DIVIDIR UM NÚMERO INTEIRO POR UM NÚMERO DECIMAL
1
Multiplicar o divisor pela unidade seguida por tantos zeros quanto os dígitos decimais que queremos eliminar (3,6 x 10 = 36).
2
Multiplicar o dividendo pelo mesmo número que multiplicamos o divisor (278 x 10 = 2780).

Quando colocar uma vírgula na divisão?

A divisão é uma das quatro operações básicas da matemática e é inversa à multiplicação. A divisão de um número consiste em seu fracionamento, na sua fragmentação, que pode ter como resultado um número inteiro ou um número decimal.

Assim como as outras operações fundamentais da matemática, a divisão também está muito presente em nosso cotidiano, por isso, é essencial conhecer bem esse processo, a fim de adquirir prática e tornar esse cálculo mais ágil.

Quando vamos dividir um número P por um número d, devemos buscar um número q que multiplicado por d seja igual a P. Cada um desses elementos recebem um nome: P é chamado de dividendo, d é o divisor e q o quociente.

Nem sempre é possível encontrar esse número q, em alguns casos, a multiplicação de d por q apenas fica muito próxima de P. Nessas situações, a diferença de P pelo resultado da multiplicação de d por q é chamado de resto e será denotado por r.

a) 28: 2 = 14, pois 2 ·14 = 28 → Divisão exata

b) 29: 2 ≠ 14, pois 2 ·14 = 28 → Divisão não exata, apresenta resto = 1

Quando o resto não aparece, ou seja, quando r = 0, dizemos que o número P é divisível por d. Caso contrário, P não é divisível por d.

Podemos afirmar que:

P = d ·q + r

Vejamos agora um método que facilita encontrar todos esses elementos: método da chave. Veja a figura abaixo:

Na divisão do número 25 por 5 temos:

O número 25 é o dividendo, o número 5 é o divisor, 5 é o quociente, e zero é o resto da divisão. Note que para realizar a divisão é necessário encontrar um número que multiplicado por 5 seja igual a 25, nesse caso, o número é o próprio 5.

Veja também que podemos escrever o número 25 da seguinte maneira:

25 = 5 · 5 + 0

Para facilitar o processo de divisão, temos um algoritmo, isto é, temos um passo a passo que pode facilitar. Para verificarmos esse processo, vamos tomar a seguinte divisão 64: 4.

Primeiro passo: montar a operação utilizando o método da chave.

Segundo passo: tentar encontrar um número que multiplicado por 4 seja igual a 64. Como essa não é uma tarefa fácil, vamos tomar somente o número 6 para dividir com o número 4, ou seja, o algarismo da dezena. Assim, devemos determinar um número inteiro que multiplicado por 4 seja igual a 6 ou que chegue o mais próximo possível.

Terceiro passo: prosseguir a divisão descendo o algarismo da unidade, que não foi dividido, nesse caso, o 4.

O processo chega ao fim, quando obtemos que o resto é igual a 0. Caso contrário, devemos continuar a divisão seguindo os mesmos procedimentos.

Na divisão de números inteiros, devemos ficar atentos quanto aos sinais. Devemos lembrar-nos das propriedades dos números inteiros:

Sinal do primeiro número
Sinal do segundo número
Sinal do resultado

a) (+ 55) : (+11) = +5

b) (+243) : (– 3) = – 81

c) (– 1050) : (+5) = – 210

d) (– 12) : (– 6) = +2

Na divisão, há duas situações possíveis: divisão exata e divisão não exata, que apresenta resto.

Como multiplicar dois números com vírgula?

Multiplicação com vírgula: Entenda tudo de maneira simples

Neste post vamos explicar como fazer multiplicação com decimais. É muito simples!

Para realizar a multiplicação com decimais, basta realizar, primeiramente, a multiplicação normal dos dois números, como se não tivessem vírgula. Ou seja, alinham-se os dois números pela casa da direita e inicia-se a multiplicação como se fossem números inteiros.

Após realizar a multiplicação, é só colocar a vírgula no lugar certo do resultado: o número resultante terá tantas casas decimais quanto forem a soma do número de casas decimais dos fatores.

Exemplo

Calcular o produto: 4,281 x 72,5

Primeiro, realizaremos o produto dos dois números desconsiderando as vírgulas, como se fossem dois números inteiros:

4,281 x 72,5 = 3103725

Após obter o resultado da multiplicação, que neste caso foi 3103725, partimos para a colocação da vírgula. Os números que multiplicamos são:

• 4,281: tem 3 casas decimais
• 72,5: tem 1 casa decimal

Portanto, o resultado terá 3 + 1 = 4 casas decimais, ou seja, o resultado tem o número de casas decimais igual à soma das casas decimais dos números que estamos multiplicando. Portanto, o resultado desta multiplicação é: 310,3725.

Para aprender com exemplos estas e muitas outras operações fundamentais, acesse já o Stoodi e cadastre-se.

Como fazer o cálculo da divisão?

A divisão é operação matemática utilizada para descobrir como separar uma quantidade em partes, ou seja, “fracionar” algo.

Geralmente, o símbolo utilizado para a operação é ÷, mas também podemos encontrar casos em que : e / são utilizados como sinal de divisão.

Por exemplo, podemos indicar uma divisão simples da seguinte forma:

• 31 ÷ 3 = 10
• 4 : 2 = 2
• 5 / 5 = 1

Os nomes dos termos de uma divisão são: dividendo, divisor, quociente e resto. Veja no exemplo a seguir.

Sendo assim, podemos escrever a conta de divisão da seguinte forma:

dividendo / divisor = quociente

14 / 2 = 7

Observe que na divisão de 14 por 2 obtemos uma divisão exata, pois não existe resto.

A divisão exata é a operação inversa da multiplicação, pois a multiplicação de quociente e divisor tem como resultado o dividendo.

quociente x divisor = dividendo

7 x 2 = 14

Se uma divisão apresentar resto então ela é classificada como não exata. Por exemplo, a divisão de 37 por 15 não é exata, já que tem resto diferente de 0.

Dessa forma, podemos relacionar os termos da divisão assim:

quociente x divisor + resto = dividendo

2 x 15 + 7 = 37

Saiba o que são os divisores.

Confira alguns exemplos de divisão e as regras para efetuar essa operação matemática.

As regras para dividir números inteiros são:

1. 1º: organize a operação identificando o dividendo e o divisor;
2. 2º: encontre um número que multiplicado pelo divisor seja igual ou próximo ao dividendo;
3. 3º caso o número seja menor que o dividendo subtraia um pelo outro e continue a divisão com o resto até que não haja mais nenhum número para continuar a divisão.

Exemplo: 224 ÷ 8

Como chegamos ao resto 0, temos uma divisão exata. Observe que 224 é divisível por 8, pois 28 x 8 = 224.

Leia também sobre múltiplos e divisores.

Quando a divisão não é exata, podemos continuar realizando a operação com o resto, mas obteremos um quociente decimal.

Para isso, adicionamos um 0 ao resto para continuar a divisão e devemos colocar uma vírgula no quociente para prosseguir a operação.

Exemplo: 31 ÷ 5

Portanto, 31 ÷ 5 é uma divisão com quociente decimal.

Na divisão em que o dividendo e o divisor são decimais devemos iniciar eliminando a vírgula do divisor. Para isso, contamos o número de casas após a vírgula e “andamos” o mesmo número de casas no dividendo.

Exemplo: 2,5 ÷ 0,25

Observe que no divisor após a vírgula temos dois algarismos. Assim, movemos a vírgula duas casas no divisor e no dividendo. Logo, 2,5 ÷ 0,25 se transforma em 250 ÷ 25, ou seja, é como se multiplicássemos os dois números por 100.

Logo, 2,5 ÷ 0,25 = 250 ÷ 25 = 10.

Saiba mais sobre a divisão com vírgula.

Na divisão de números com sinais diferentes devemos levar em consideração a regra dos sinais para determinar o resultado.

Para esse tipo de divisão temos as regras:

1. Divisão de números positivos (+) resulta em um quociente positivo (+);
2. Divisão de números negativos (-) resulta em um quociente negativo (-).

Confira alguns exemplos:

22 ÷ 11 = 2

(– 10) ÷ (– 5) = 2

30 ÷ (– 15) = – 2

(– 40) ÷ 20 = – 2

Não esqueça que quando um número é positivo (+) não é necessário colocar o sinal antes dele.

Veja também: Tabuada

Antes de começar vamos nomear os termos de uma fração com o exemplo a seguir.

Para rea”.

Como fazer divisão de números decimais 5 ano?

A divisão é uma operação matemática que consiste em “fracionar” um número em partes iguais. Muitas vezes a divisão não é exata e para continuá-la é necessário adicionar uma vírgula ao quociente.

A vírgula também pode estar presente nos outros termos da divisão (dividendo e divisor), ou seja, uma divisão de números decimais.

Antes de vermos os exemplos, relembre os termos da divisão com a imagem a seguir.

Nesse tipo de divisão os dois termos devem ter o mesmo número de algarismos depois da vírgula para que ela seja eliminada.

Por exemplo, quando o dividendo e o divisor são números decimais com um algarismo após a vírgula podemos multiplicar ambos por 10 para que a vírgula seja eliminada e os números se transformem em números inteiros.

Exemplo 1: 2,5 ÷ 0,5

Portanto, 2,5 ÷ 0,5 = 5

Exemplo 2: 2,42 ÷ 0,22

Neste caso temos dois algarismos após a vírgula. Portanto, podemos multiplicar os dois termos por 10 duas vezes, que é o mesmo que multiplicar 100, para eliminar a vírgula.

Note que cada vez que multiplicamos por 100 “andamos” com a vírgula duas vezes. Após isso, podemos efetuar a divisão.

Portanto, 2,42 ÷ 0,22 = 11.

Para a divisão de um número decimal ser efetuada é necessário reescrever o divisor para que ele também apresente o mesmo número de casas decimais do dividendo e, assim, a vírgula possa ser eliminada.

Exemplo: 12,5 ÷ 5

Primeiramente, devemos reescrever o divisor de forma que ele também apresente o mesmo número de casas decimais que o dividendo.

12,5 ÷ 5 → 12,5 ÷ 5,0

Agora, eliminamos a vírgula multiplicando os dois termos por 10, já que ambos apresentam uma casa decimal.

Observe que na divisão chegamos ao resto 25. Para continuá-la devemos adicionar uma vírgula ao quociente e um zero ao resto.

Sendo assim, 12,5 ÷ 5 = 2,5.

A divisão por um número decimal ocorre quando o divisor apresenta uma vírgula e para resolvê-la devemos adicionar uma vírgula ao dividendo e, em seguida, o número de zeros que corresponde ao número de casas decimais depois da vírgula no divisor.

Exemplo: 120,6

Note que o divisor tem uma casa decimal após a vírgula. Reescrevendo o dividendo, temos:

12 ÷ 0,6 → 12,0 ÷ 0,6

Para eliminar a vírgula, multiplicamos os dois termos por 10 e depois efetuamos a divisão.

Portanto, 12 ÷ 0,6 = 20.

Uma divisão não exata ocorre quando um número inteiro é dividido por outro número inteiro e há resto na divisão. Temos então uma divisão com quociente decimal.

Para continuar a divisão:

Exemplo: 196 ÷ 5

Observe que a divisão de 196 por 5 é uma divisão não exata com resto 1. Para continuar a divisão adicionamos um 0 ao resto e a vírgula no quociente, ou seja, o algarismo 2 deve estar na casa dos décimos.

Podemos interpretar essa divisão da seguinte forma: se um valor de R$ 196 fosse dividido para 5 pessoas, cada uma receberia trinta e nove reais e vinte centavos.

Quando o dividendo é menor que o divisor devemos adicionar um zero e uma vírgula ao quociente e também um 0 ao dividendo antes de iniciar a divisão. Neste caso teremos um quociente decimal.

Como e feita a divisão de números decimais?

A divisão é a operação matemática básica mais difícil e um dos conceitos mais complicados do Ensino Fundamental. Diferentemente das outras operações, o algoritmo utilizado para resolvê-la envolve uma série de regras para casos específicos de números presentes no divisor e/ou no dividendo. Uma dessas regras refere-se à divisão com números decimais.

Desse modo, discutiremos uma das técnicas mais eficazes para a divisão envolvendo decimais.

Divisão com números decimais:

Para dividir números decimais, é necessário conhecer o procedimento adequado quando o divisor é maior que 10.

O procedimento adequado para divisão com números decimais é feito com os seguintes passos:

1. Contar as casas decimais do divisor e do dividendo e escolher o maior entre esses números;
2. Calcular a potência 10n, sendo n o número escolhido no passo anterior;
3. Multiplicar divisor e dividendo pelo resultado dessa potência;
4. Realizar a divisão propriamente dita.

Para cumprir o último passo, utilizaremos o método da chave, também conhecido como algoritmo da divisão, que é a técnica mais utilizada no Brasil.

Exemplo 1:

Calcule a divisão de 3,82 por 0,2.

Vamos seguir os passos apresentados anteriormente:

1. O divisor possui uma casa decimal, e o dividendo, duas. Portanto, escolheremos o número 2 para o passo seguinte;
2. Para cumprir esse passo, faremos 10² = 100;
3. Basta calcular 3,82·100 = 382 e 0,2·100 = 20.
4. Observe que não existem mais vírgulas no resultado. Como ambos foram multiplicados pelo mesmo número, seus resultados serão iguais. Desse modo, realizando a divisão de 382 por 20, obteremos o mesmo resultado que na divisão de 3,82 por 0,2. Portanto:

382 | 20

– 20    19

182

– 180

2

Se for necessário prosseguir dividindo, utilize o procedimento adequado para divisão com resultado decimal.

Exemplo 2:

Sabendo que a área de um retângulo é 544,214 m² e que sua largura mede 15,4, determine a medida de seu comprimento.

Sabendo que a área é o produto da largura pelo comprimento, para encontrar uma dessas duas últimas, basta dividir o valor da área pela outra. Desse modo, para descobrir o comprimento do retângulo, devemos dividir área pela largura. Seguindo os passos apresentados acima, teremos:

1. O divisor possui uma casa decimal, e o dividendo, três. Desse modo, escolheremos o número 3 para o passo seguinte;
2. Observe que 10³ = 1000;
3. 544,214·1000 = 544214 e 15,4·1000 = 15400;
4. 544214 | 15400

– 46200        35

82214          

– 77000             

5214

Como saber onde colocar a vírgula na divisão?

Ao aprender sobre a operação da divisão, sabemos que existem divisões exatas e divisões não exatas (quando há um resto na divisão). Por exemplo, se quisermos dividir 5 por 2, teremos uma divisão não exata, pois haverá um resto. Mas existe uma possibilidade de terminar essa divisão? Se você tem cinco reais, é possível dividir esse valor para dois amigos? Claro! Cada amigo ganhará dois reais e cinquenta centavos. O “um real” que ficaria no resto foi dividido igualmente e agora não há mais restos nessa divisão. Vejamos outro cálculo semelhante a esse: a divisão de 225 por 50. Se multiplicarmos 4 por 50, obteremos 200, e assim a divisão terá resto 25. Não existe um número natural que multiplicado por 50 resulte em 25, então, qualquer valor que acrescentarmos ao quociente será menor do que 1. Portanto, para prosseguirmos, teremos uma divisão com vírgula, pois acrescentaremos uma vírgula ao quociente e um zero ao resto. Procuramos agora um número que multiplicado por 50 resulte em 250. Esse número é o 5. Portanto, 225 : 50 = 4,5.

Para que não haja resto na divisão, nós acrescentamos a vírgula ao quociente para continuar uma divisão que seria inexata. Vamos agora realizar a divisão de 201 por 4. Essa também é uma divisão não exata e deixará resto 1. Quando estivermos próximos de finalizar a divisão e encontrarmos o resto, será necessário acrescentar uma vírgula ao quociente e um zero no fim do resto. A partir daí, basta realizar a divisão normalmente até que não haja resto algum. Nesse caso, há uma divisão com vírgula, pois a divisão de 201 por 4 resulta em 50,25.

Novamente, para que não haja resto na divisão, nós acrescentamos vírgula ao quociente para completar a divisão. Mas e quando o dividendo ou o divisor é um número decimal (com vírgula)? Precisamos lembrar que um número decimal só divide ou é dividido por outro número decimal se houver a mesma quantidade de algarismos depois da vírgula. Se um dos fatores da divisão é um número decimal, devemos escrever o outro na forma decimal também. Por exemplo, o número 2 pode ser escrito como 2,0; 2,00; 2,000…

Vejamos como realizar a divisão de 3,4 por 2. O primeiro passo é observar que, como o 3,4 é um número decimal com um algarismo depois da vírgula, o 2 deve ter esse mesmo formato, por isso utilizamos o 2,0 no divisor. Agora que ambos os fatores da divisão possuem a mesma quantidade de algarismos depois da vírgula, nós podemos desconsiderar as vírgulas e realizar a divisão de 34 por 20, obtendo como resultado 1,7. Veja na imagem a seguir todo o processo para realizar essa divisão:

Precisamos escrever o divisor na forma decimal com um algarismo após a vírgula para então descartar as vírgulas e realizar a divisão.

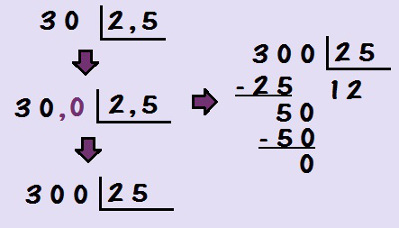
Imagine uma situação nova: no dividendo, há o número natural 30, e no divisor, um número racional 2,5. Lembre-se de que um número decimal só divide ou é dividido por outro número decimal se ambos possuem a mesma quantidade de algarismos após a vírgula. Para realizar a divisão, vamos escrever o número.

Como fazer a divisão de um número inteiro por um número com vírgula?

DIVIDIR UM NÚMERO INTEIRO POR UM NÚMERO DECIMAL
1
Multiplicar o divisor pela unidade seguida por tantos zeros quanto os dígitos decimais que queremos eliminar (3,6 x 10 = 36).
2
Multiplicar o dividendo pelo mesmo número que multiplicamos o divisor (278 x 10 = 2780).